Return to the main Sudoku Analyzer page.
The following explanation assumes that you are already familiar with CyberJerry's Elimination Grid and the basics of pencilling in all possible candidates for each unsolved cell. Even more than with other advanced techniques, the MutEx method requires one to be very thorough and careful at each step.
To employ the MutEx technique on paper, you will construct 2-color chains of mutually exclusive pairs by highlighting the numeric candidates with transparent markers of contrasting colors, or circling them with crayons or colored pencils. Erasable markers or pencils are advised. You may need additional contrasting colors for constructing tentative secondary chains.
Begin by recognizing two situations in which two candidates are mutually exclusive. In both cases, one number must be true, and the other false. We can highlight the two candidates with contrasting colors to illustrate this mutually exclusive relationship:
| A. An unsolved cell with exactly two possible candidates. |  example A |
B. A number that occurs exactly twice in a given row, column, or 3x3 box. | 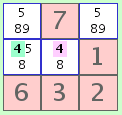 example B |
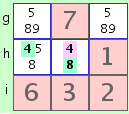 fig. 1a |
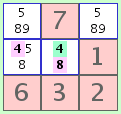 fig. 1b |
Now notice that we can chain A and B together as illustrated in figure 1a. Since both the '8' in the middle cell and the '4' in the left cell are linked to the middle '4' in a mutually exclusive relationship, they must both be colored the same. If the pink '4' is true, the green '4' and green '8' must both be false. If the pink '4' is false, both green numbers must be true. This means, in effect, that if the '4' in the left cell is true, the '8' in the middle cell must also be true, and vice-versa. Likewise if one is false, they must both be false. Since the choice of colors is arbitrary, figure 1b also validly demonstrates the mutually exclusive relationships between candidates.
CyberJerry's help (in the 'Messages' area) might describe the above chain thus:
8@h2 -> 4@h2 -> 4@h1which is a shorthand way of saying, "The '8' in cell h2 is mutually exclusive with the '4' in cell h2 which in turn is mutually exclusive with the '4' in cell h1".
Or, it might say:
4@h2 -> 8@h2, 4@h2 -> 4@h1which is, "The '4' in cell h2 is mutually exclusive with the '8' in cell h2, and the '4' in cell h2 is also mutually exclusive with the '4' in cell h1".
[Note 2] Internal conflicts:
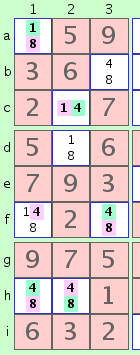
fig. 2
8@f3 -> 4@f3 -> 4@f1 -> 4@h1 -> 8@h1 -> 8@h2 -> 4@h2 -> 4@c2 -> 1@c2 -> 1@a1 -> 8@a1which indicates that, starting with the '8' in cell f3, we can link to the '4' in f3 (per example A above), then to the '4' in cell f1 (per example B), and so on to successive candidates, alternating colors until we come to the pink '8' in cell a1. At that point we get the following conflict:
Now apply the following logic:
- Since the two colors represent two mutually exclusive possibilities, the 6 pink candidates must all be true or all false. (The chain)
- The two pink '8's cannot both be true since they occur in the same column. (The conflict)
- Therefore, the two pink '8's must both be false.
- Since the chain represents two mutually exclusive possibilities, all 6 pink candidates must be false.
- More importantly, the 5 green candidates must therefore be true.
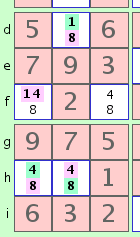
fig. 2a
1@f1 -> 1@d2 -> 8@d2 -> 8@h2 -> 4@h2 -> 4@h1 -> 8@h1, 4@h1 -> 4@f1which produces the following conflict:
This conflict is a bit more obvious than that of fig. 2, while producing pretty much the same end result.
[Note 3] External conflicts:
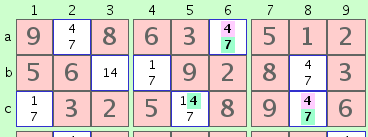
fig. 3
Although this short chain contains no internal conflicts, it produces the following:
Our 2-color system makes it easy to see that the 2 green '7's must both be true or both false, and they cannot both be true, since that would result in an unsolvable top left 3x3 square. So the 2 pink candidates must be true, and we have thus solved two cells in one stroke.
[3a]
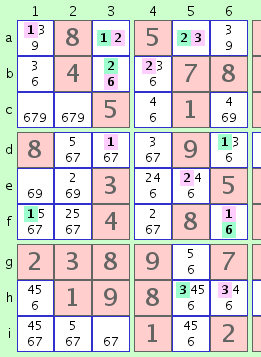
fig. 3a
If the green candidates were true, cell d6 would be a '1'. If the pink candidates were true, cell h6 would be a '3'. In either case, cell d6 could not be a '3'.

fig. 3b
Only one place for a '3' in the middle 3x3 square.which is to say, we've solved cell d4. It's a '3'.
[Note 3c] Extending the chain:
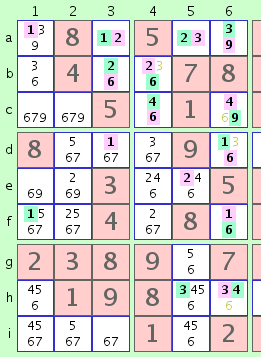
fig. 3c
Now we have both a green '6' and a pink '6' in column 6. Using the same logic as above, we can eliminate the other two '6's in column 6 - those in cells c6 and h6. This, in turn, allows us to further extend the chain as follows:
3@h6 -> 4@h6 -> 4@c6 -> 9@c6 -> 9@a6 -> 3@a6, 4@c6 -> 4@c4 -> 6@c4 -> 6@b4This extended chain, as shown in fig. 3c., now allows us to eliminate the '3' in cell b4, and perhaps other eliminations and/or extensions.
[Note 4] Comparing 2 chains:
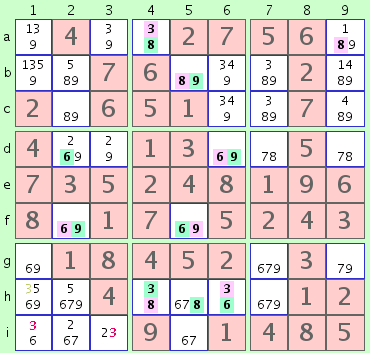
fig. 4
(By the way, notice also that before forming the link 3@h4 -> 3@h6 which forms an important part of this chain, we had to have first eliminated the '3' in cell h1 by means of the 'Box/Line' technique.)
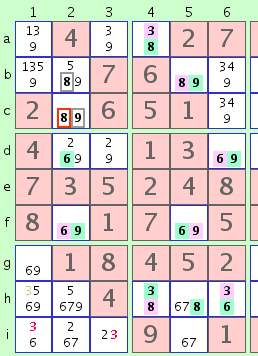
fig. 4a
This gives us an interesting situation. Although both chains are complete and contain no conflicts when considered singly, together they produce the following conflict:
Notice two conflicts between candidates of the two chains: The '8' in cell b5 (chain 1) and the '8' in b2 (chain 2) cannot both be true. Likewise the '9' in f2 (chain 1) and the '9' in c2 (chain 2). The inter-chain conflict is this: since the two candidates in the first chain are mutually exclusive, one of them must be true. But the two candidates in the second chain are colored alike and so must be of the same veracity; either both are true or both false. The only way one of the mutually exclusive numbers in the first chain can be true is if the two grey numbers in the second chain are both false. Since the grey numbers are false, the red one (the '8' in cell c2) must be true, and we've solved that cell.
As noted above, the MutEx technique requires plenty of patience and thoroughness. You may have to construct several chains before finding a chain or pair of chains with a conflict that allows you to solve even a single cell. But then your patience and thoroughness may often result in several solved cells in one stroke. So, while I cannot guarantee that the MutEx method will solve every Sudoku with unfailing success, I can say that it seems to be the Sudoku method of final resort, enabling a step-by-step solution to some very tough and otherwise unsolvable Sudokus.
I am well aware that various versions of the mutually exclusive two-color strategy may be suggested by other Sudoku experts. Well, Ok. I humbly believe that my 'MutEx' method combines pretty much all these 2 color techniques into one comprehensive strategy. If you disagree, I'd be eager to hear from you. Also welcome are more general inquiries and suggestions. You may use this website's Contact page for various ways to reach me.